Generative models basics

Understanding generative models

List of common buzz words

• vanishing gradient
• Batch normalization
• Latent space
• Upsampling
• Increasing/decreasing channels and spatial shape
• LSTM/GRU

Representation learning - mapping high dimensional data to latent space(lower dimmensional)

Latent space: refers to an abstract multi-dimensional space containing feature values that we cannot interpret directly, but which encodes a meaningful internal representation of externally observed events.

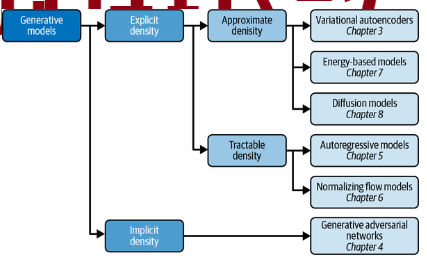
Implicit models - producing stochastic prcess that generates data - GAN

Tractable models - density function has form easy to calculate

• autoregressive models impose order of input features
• nomralizing flow - series of tractable, invertible functions
• approximate density models - variational autoencoders - approx joint denisty function with latent variable
• energy based - markov chains

Autoencoder

• encoder - converts input to embending latent vector(of lower dimensionality)
• decoder can be used to generate new images - probing latent space
• can be used as denoisers - autoencoder learns that is not useful to learn

Encoder

• consist of input, hidden layers of types
  • dense - tabular, flattened
  • convolutional - spatial
  • recurrent - sequential data, temporal dynamic
  • transformer - sequential data, self attention, long range dependencies
• bottleneck - reduces dimensionality to final latent representation

Decoder

• mirror image of encoder
• need for Conv2DTranspose - allows for upsampling information

GAN

Discriminator

• predicts if observation is from original distribution
• solves supervised classification problem
• similar to encoder - reduces spatial shape while increasing number of channels, but has one number at the end
• learning: images from real dataset and from generator with labels

Generator

• converts random noise into observations
• input is vector taken from multivariate standard normal distribution
• increases spatial shape while decreasing number of channels
• learning: loss function is output of discriminator

Problems

• discriminator overpowers generator - try to weaken discriminator - stronger dropout, smaller learning rate, less cnn filters, noise to labels, flipping labels at random
• generator overpowers discriminator(mode collapse) - generator finds single observation(mode) that always fools discriminator → every point in latent spaced mapped to that observation
• uninformative loss - generator loss has to increase - discriminator becomes better at distingishing input but that also means generator becomes better at generating images

Wasserstein GAN with Gradient Penalty

• meaningfull loss metric that correlates with generator convergence
• better stability of learning

LSTM

LSTM cell

• cell state - aggregated of data from previous processed steps
• hidden state - encoding of recent time-step
• Consist of gates of formula $f_t=\sigma((W_{hf} \times h_{t-1})+(W_{xf} \times x_t)+b_f)$
• Forget gate - tells how important is aggregated history
• Input gate - tells how much input should change internal cell state
  • Input node - tanh activation - $\tilde{C}$
• Output gate - how important is internal state for whole cell output

Cell internal state $C_t=F_t \odot C_{t-1}+ I_t \odot \tilde{C}$

Hidden state $H_t = O_t \odot tanh(C_t)$

(sigmoid func - amplify/diminish; tanh func - transform into normalized encoding of data)